Le forum de XCAS

Hello BP, a small improvement in the command

if the simplification flag is none return

canonical_form(x^2-6*x) returns (x-3)^2-(-6/2)^2 // “completing the square.”

this allows to show in the classroom, steps as if they were done by hand

current

canonical_form(x^2-6*x) returns (x-3)^2-9

? What the point of not simplifying 6/2?
Anyway, giac reduces rational fractions of integers always.

Leaving the 6/2 unsimplified shows a middle step in the complete the square formula
x^2 + b^x = (x + (b/2))^2 - (b/2)^2
If having simplify set to none would do that, then (I would think) that going through all the steps would require
switching between simplification modes. It might anyhow be easier to write a function
complete_square_step
that (after checking for the variable, making sure you have a second degree polynomial, making it monic, etc.)
returns
(x + quote(coeff(expr,x,1)/2))^2 + (coeff(expr,x,0) - (quote(coeff(expr,x,1)/2)^2)
or something. And then simplify that to finish it.

I think there should be a new mode: "Didactic CAS"

Source:
free book "Doing Mathematics withScientic WorkPlace"
https://www.sciword.co.uk/manuals/


expr0:=x^2-6*x;
(x + (coeff(expr0,x,1)/2))^2 + (coeff(expr0,x,0) - ((coeff(expr0,x,1)/2)^2)); returns
(x-3)^2-9

(x + quote(coeff(expr0,x,1)/2))^2 + (coeff(expr0,x,0) - (quote(coeff(expr0,x,1)/2)^2)) returns
(x+coeff(expr0,x,1)/2)^2-(coeff(expr0,x,1)/2)^2

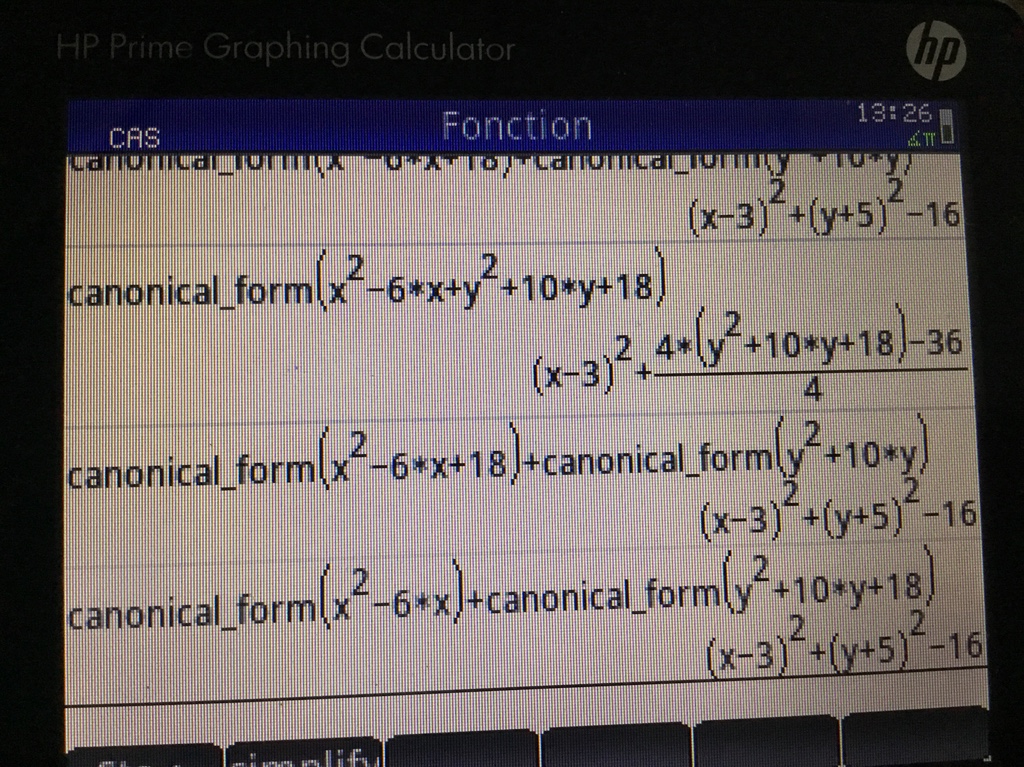
canonical_form(x^2-6*x+y^2+10*y=18) returns " Error: Bad Argument Value"

canonical form x^2-6*x+y^2+10*y=-18 http://www.wolframalpha.com/input/?i=ca ... 10*y%3D-18
(x - 3)^2 + (y + 5)^2 - 16 = 0

canonical_form(x^2-6*x+y^2+10*y+18) " returns
(x-3)^2+(4*(y^2+10*y+18)-36)/4

I disagree with the idea that one should keep 6/2 unsimplified in the constant square. As an intermediate step to build the square containing x canceling the linear term, that's acceptable, but not after in my opinion. Anyway, as I explained, Xcas is designed from scratch to simplify rationals, it can not be changed.

an idea, for expressions of more than one variable, the second argument would specify the "subpolynomy"

canonical_form(x^2-6*x+y^2+10*y+18 , x ) => canonical_form(x^2-6*x, x ) + y^2+10*y+18 => (x-3)^2-9 + y^2+10*y+18

canonical_form(x^2-6*x+y^2+10*y+18 , y ) => canonical_form(y^2+10*y+18 , y )+x^2-6*x => (y+5)^2-7 + x^2-6*x

canonical_form(x^2-6*x+y^2+10*y+18 , [x,y] ) => canonical_form(x^2-6*x, x )+canonical_form(y^2+10*y+18 , y ) => (x-3)^2 + (y+5)^2 -16

I don't understand your question, canonical_form already accepts a 2nd argument (the variable with respect to which the canonical form is computed).